高斯分布是什么？一文了解应用场景、公式推导及常见误区解析

高斯分布（又称正态分布）是统计学和数据科学领域最基础且广泛应用的概率模型，其“钟型曲线”描述了众多自然现象与社会数据的分布规律。本文以新闻深度报道角度，系统解析高斯分布的基本原理、数学公式、经典应用场景与行业误区，并结合专家观点和实际案例，帮助你全面掌握高斯分布在当今AI、金融、工业中的核心价值。

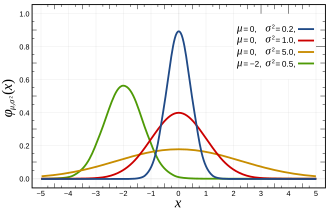
高斯分布基本概念与公式推导

高斯分布是什么？定义与特点

高斯分布，又称“正态分布”（Normal Distribution），是概率论和统计学中极为重要的连续型分布，其概率密度函数呈标准“钟型曲线”，左右对称，均值处取最大概率。命名来源于德国数学家卡尔·弗里德里希·高斯。

数学历程：概率密度函数推导

一维高斯分布（正态分布）的概率密度函数为：

$
f(x) = \frac{1}{\sigma\sqrt{2\pi}}  \exp\left( -\frac{(x-\mu)^2}{2\sigma^2} \right)
$

• μ（均值）：决定分布的中心。
• σ（标准差）：决定分布宽窄，σ越小曲线越高越窄，σ越大则越平坦。

当μ=0、σ=1时，称为标准正态分布。

与AI角色无限畅聊，开启你的专属故事

海量二次元、三次元角色等你互动，体验真正无限制的AI角色扮演对话。立即加入，新用户登录即送6000积分！

如何游玩？立即免费体验 →

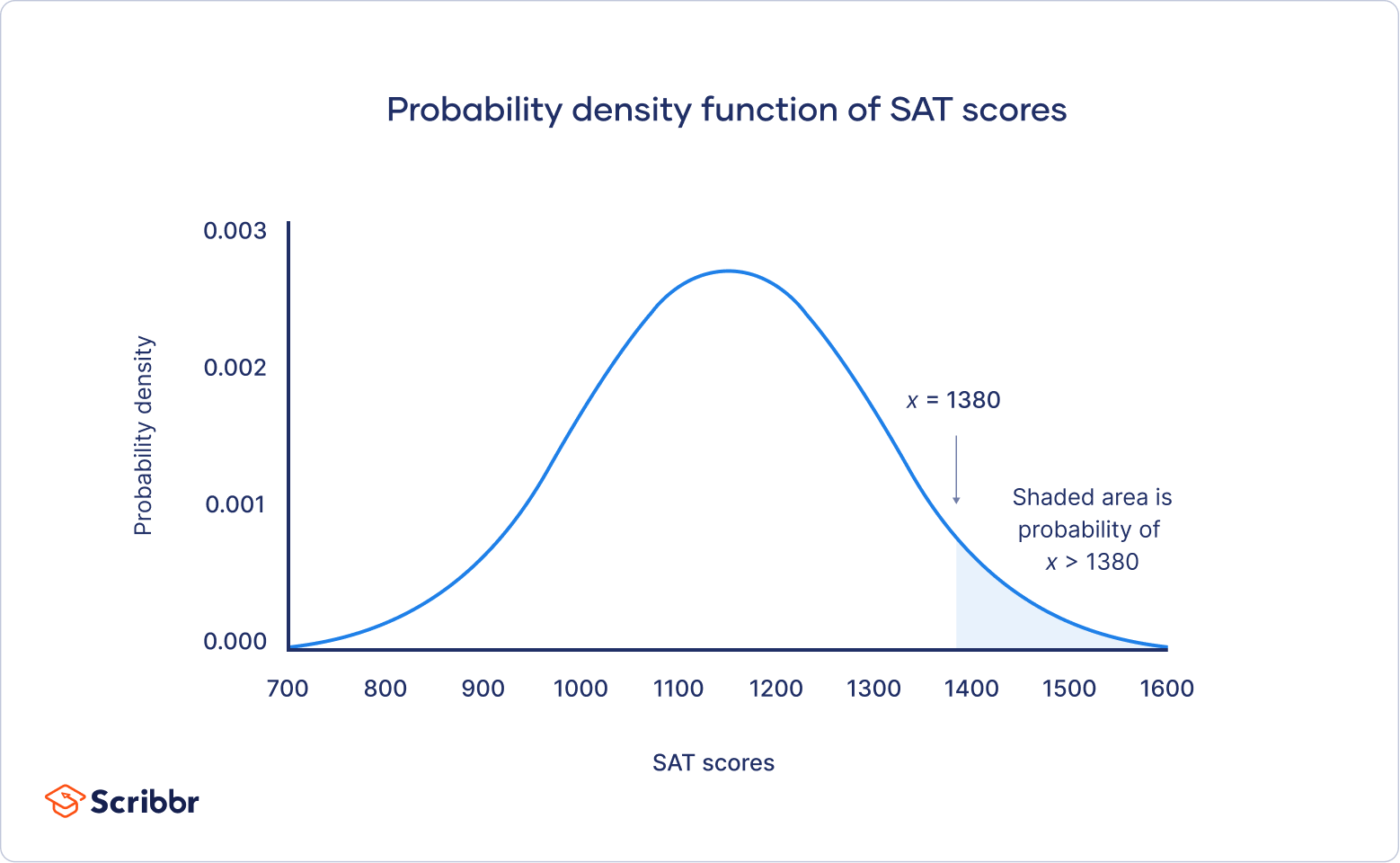
标准正态分布与数据覆盖率

• 约68.27%的数据在[μ−σ, μ+σ]范围内；
• 约95.45%在[μ−2σ, μ+2σ]；
• 约99.73%在[μ−3σ, μ+3σ]。

多元高斯分布

当多个变量联合服从高斯分布时，采用多元高斯分布：

$
f(\mathbf{x}) = \frac{1}{ (2\pi)^{k/2}|\Sigma|^{1/2}} \exp\left(-\frac{1}{2}(\mathbf{x}-\mu)^T \Sigma^{-1} (\mathbf{x}-\mu) \right)
$

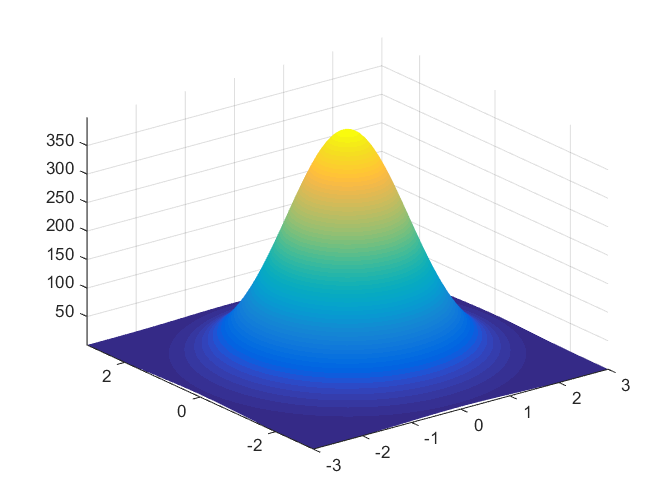
• Σ为协方差矩阵，k为维数

高斯分布的应用场景大盘点

中心极限定理解释了高斯分布为何“无处不在”，只要独立同分布变量样本足够大，其和或均值趋于高斯分布。

质量检测：工业标准与自动化

高斯分布用于评估产品指标（如尺寸、重量）是否在可接受范围。例如螺丝长度μ=10mm，σ=0.05mm，可设置标准警戒线。

教育评分：曲线评定法

大型考试（如高考）常假定成绩呈高斯分布，通过统计参数核算各分段赋值，以减少极端分数带来的评价误导。

人工智能与深度学习

• 神经网络权重初始化（如PyTorch、TensorFlow的normal随机函数）
• GAN/VAE中噪声样本生成
• 机器学习算法中的参数最大似然估计

数据预处理与异常检测

在金融、网络安全等行业，若数据服从高斯分布，则超出[μ±3σ]的点极有可能是异常，需重点关注或剔除。

高斯分布的常见误区揭秘

AI工具推荐：自动检定数据正态性，可使用Statistical Tests AI批量做Shapiro-Wilk或Anderson-Darling测试。

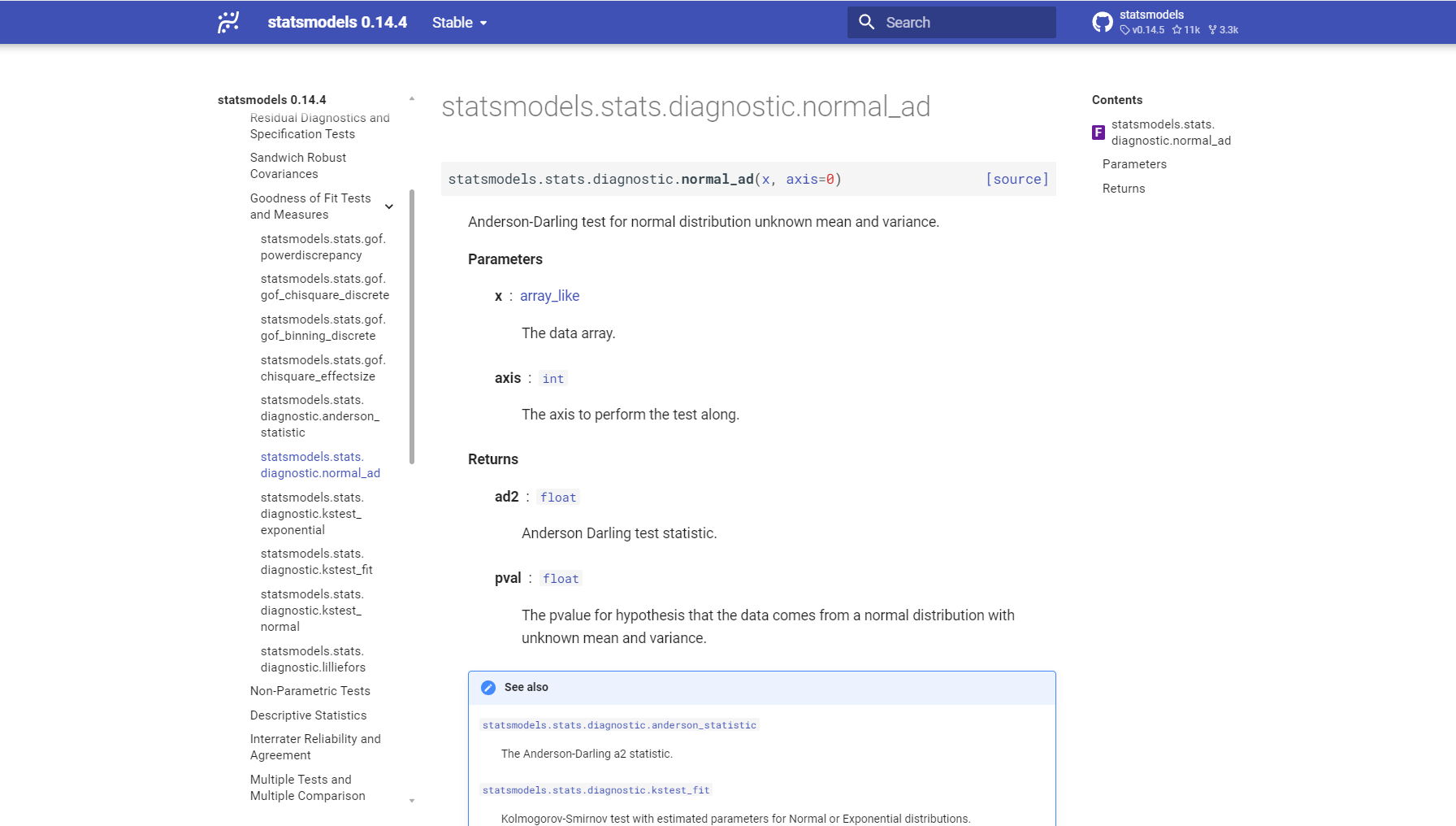
行业专家观点：高斯分布的时代价值

知名人工智能专家何教授表示：“高斯分布早已嵌入科学计量、金融、智能诊断、图像识别等每一环节。随着数据量增大与算法优化，正确选用分布假设与防范异常尤为重要。”忌盲目依赖高斯假设，建议结合偏度厚尾等敏感检验。

高斯分布相关算式与AI平台整理

媒体案例追踪：现实中的高斯分布

案例1：金融风险管理失误

某国际银行仅用高斯分布估算亏损风险，忽略“胖尾”，在2008年次贷危机造成巨量损失，成为正态假设的反思案例。

案例2：工业自动化生产

丰田汽车每道工序用高斯分布设定警示边界，精准管控品质并提前发现设备故障。

案例3：AI图像处理

高斯模糊是降噪常用算法，如OpenCV的cv2.GaussianBlur在去除图像高频噪声、提升边缘检测稳定性方面效果突出。

小知识快问快答

在数字智能时代，高斯分布的核心价值已远超统计学，贯穿人工智能、工业、风控等关键领域。科学理解其本质与边界是每位数据从业者的必修课！

与AI角色无限畅聊，开启你的专属故事

海量二次元、三次元角色等你互动，体验真正无限制的AI角色扮演对话。立即加入，新用户登录即送6000积分！

如何游玩？立即免费体验 →